متوازي أضلاع رباعي - شكل ثنائي الأبعاد جاهز وكامل بالفهرس والمقدمة والخاتمة والمراجع
**بحث عن متوازي أضلاع رباعي – شكل ثنائي الأبعاد**
**الفهرس**
| **رقم الفصل** | **العنوان** | **الصفحة** |
| ------------- | ---------------------------------------------- | ---------- |
| 1 | المقدمة | 1 |
| 2 | تعريف متوازي الأضلاع | 2 |
| 3 | الخصائص العامة لمتوازي الأضلاع | 3 |
| 4 | أنواع متوازي الأضلاع | 4 |
| 5 | شروط متوازي الأضلاع | 6 |
| 6 | الأقطار في متوازي الأضلاع | 7 |
| 7 | مساحات متوازي الأضلاع | 9 |
| 8 | محيط متوازي الأضلاع | 11 |
| 9 | الزوايا في متوازي الأضلاع | 12 |
| 10 | استخدامات متوازي الأضلاع في الحياة اليومية | 13 |
| 11 | متوازي الأضلاع في الهندسة والرياضيات التطبيقية | 14 |
| 12 | أمثلة محلولة | 17 |
| 13 | خاتمة | 20 |
| 14 | المراجع | 21 |
1- المقدمة
يُعد **متوازي الأضلاع** أحد أهم الأشكال الهندسية في علم الرياضيات والهندسة، نظرًا لانتشاره الكبير في التطبيقات اليومية والعملية، وارتباطه المباشر بالعديد من فروع العلوم مثل الفيزياء، والهندسة المعمارية، والرسم الهندسي، والميكانيكا. يُعتبر هذا الشكل أساسًا للعديد من الأشكال الهندسية الأكثر تعقيدًا، كما يُستخدم في تصميم الأجسام، وتحليل القوى، وحساب المساحات، وغير ذلك من المجالات.
يتميز متوازي الأضلاع بخصائص هندسية فريدة تجعله لوحة أساسية لتعلم التفكير الهندسي. ويهدف هذا البحث إلى تقديم دراسة شاملة حول هذا الشكل، من حيث تعريفه، خصائصه، أنواعه، طرق حساب مساحته، محيطه، الزوايا، الأقطار، إضافة إلى تطبيقات مهمة وأمثلة محلولة تساعد في فهمه بصورة متكاملة.
2- تعريف متوازي الأضلاع
**متوازي الأضلاع** هو شكل هندسي ثنائي الأبعاد (2D) يتكوّن من **أربعة أضلاع** بحيث يكون **كل ضلعين متقابلين متوازيين ومتساويين في الطول**.
وهو يصنف ضمن **الأشكال الرباعية** التي تمتلك خصائص بنائية محددة، ويتّسم بكون زواياه قد تكون حادة أو منفرجة حسب شكل الضلعين.
تعريف آخر:
متوازي الأضلاع هو رباعي فيه كل ضلعين متقابلين مستقيمان على استقامة واحدة، أي يحافظان على نفس الاتجاه دون تقاطع.
تعريف اخر
متوازي الأضلاع هو شكل هندسي رباعي الأبعاد ثنائي الأبعاد، يتميز بأن أضلاعه المتقابلة متوازية ومتساوية في الطول، وزواياه المتقابلة متساوية، ومجموع زواياه الداخلية 360 درجة، كما أن زواياه المتجاورة متكاملة (مجموعها 180 درجة)؛ وهو يشمل أشكالاً خاصة مثل المستطيل والمربع والمعين.
3- الخصائص العامة لمتوازي الأضلاع**
يمتلك متوازي الأضلاع مجموعة من الخصائص الأساسية، ومنها:
1. **الضلعان المتقابلان متوازيان.**
2. **الضلعان المتقابلان متساويان في الطول.**
3. **الزاويتان المتقابلتان متساويتان.**
4. **كل زاويتين متجاورتين مجموعهما 180°.**
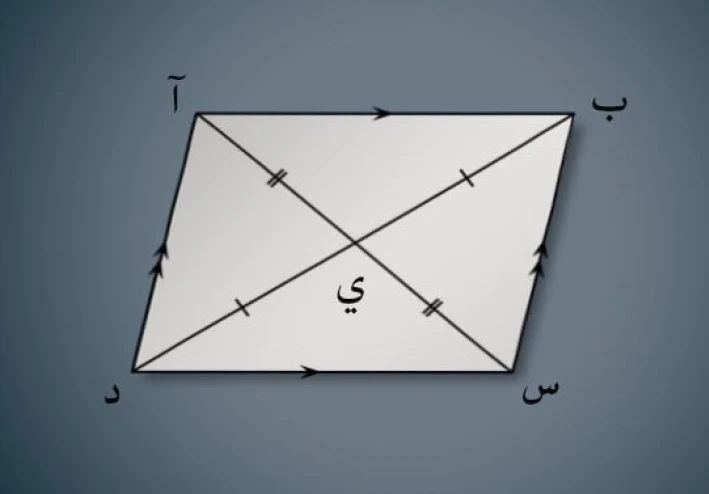
5. **الأقطار تنصف بعضها البعض.**
6. **الأقطار تقسم الشكل إلى مثلثين متطابقين.**
7. **مساحته = القاعدة × الارتفاع.**
8. يمكن رسم دائرة خارجية حوله فقط إذا كان مستطيلاً.
هذه الخصائص تساعد على إثبات أن الشكل متوازي أضلاع عند دراسة هذا النوع من الأشكال.
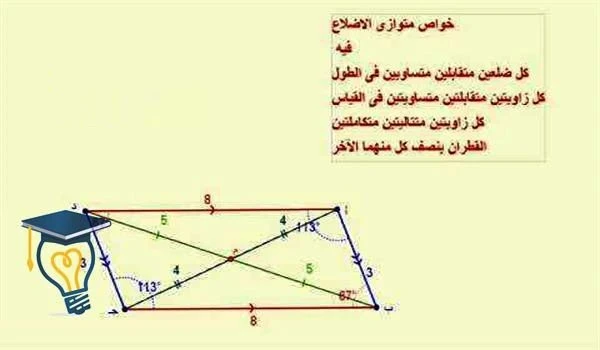
خصائص متوازي الأضلاع
- الأضلاع: كل ضلعين متقابلين متوازيان ومتساويان في الطول.
- الزوايا: كل زاويتين متقابلتين متساويتان في القياس، وكل زاويتين متجاورتين مجموعهما 180 درجة (متكاملتان).
- الأقطار: ينصف كل قطر الآخر، ويتقاطعان في نقطة تسمى مركز متوازي الأضلاع، وتكون مجموع مربعات الأضلاع مساوية لمجموع مربعي القطرين.
- المجموع الكلي للزوايا: مجموع الزوايا الداخلية لأي متوازي أضلاع هو 360 درجة.
أشكال خاصة من متوازيات الأضلاع
- المستطيل: متوازي أضلاع جميع زواياه 90 درجة، وأضلاعه المتقابلة متساوية ومتوازية.
- المربع: حالة خاصة من المستطيل والمعين، تكون جميع أضلاعه الأربعة متساوية، وجميع زواياه 90 درجة.
- المعين: متوازي أضلاع جميع أضلاعه الأربعة متساوية، وتكون أقطاره متعامدة.
أمثلة من الواقع
يمكن رؤية متوازيات الأضلاع في أشياء مثل الأبواب، النوافذ، أو حتى عندما يجلس شخص ما على كرسي مستطيل (مائل)، وتُستخدم في الرسومات لتمثيل الأجسام ثلاثية الأبعاد.
خصائص متوازي الأضلاع - BYJU'S
شكل المتوازي الأضلاع متوازي الأضلاع هو شكل ثنائي الأبعاد. له أربعة أضلاع، كل ضلعين متوازيان. كما أن الأضلاع المتوازية متساوية في ا...
متوازيات الأضلاع
مقدمة يشير متوازي الأضلاع إلى شكل هندسي ثنائي الأبعاد، حيث تكون أضلاعه المتقابلة متوازية مع بعضها البعض. هو في الواقع نوع من المضل...
نظريات حول خصائص متوازي الأضلاع - BYJU'S
خصائص مهمة لمتوازي الأضلاع متوازي الأضلاع هو شكل ثنائي الأبعاد رباعي الأضلاع مغلق، تكون فيه الأضلاع المتقابلة متوازية ...
المتوازي الأضلاع هو شكل ثنائي الأبعاد له أربعة أضلاع مستقيمة.
متوازي الأضلاع هو شكل رباعي له زوجان من الأضلاع المتوازية. يجب أن يكون الضلعان المتقابلان متساويين في الطول. لمتوازي الأضلاع أربعة رؤوس وأربعة أضلاع مستقيمة ، ...
يُعرَّف متوازي الأضلاع بأنه شكل رباعي يكون فيه كلا الضلعين المتقابلين متوازيين ومتساويين. قد تختلف الزاوية بين الضلعين المتجاورين في متوازي الأضلاع، ولكن يجب
4- أنواع متوازي الأضلاع**
هناك عدة أنواع تندرج تحت مفهوم متوازي الأضلاع، وهي:
**أولاً: المستطيل**
هو متوازي أضلاع **جميع زواياه قائمة (90°)**.
الخصائص:
* كل ضلعين متقابلين متساويان.
* الأقطار متساوية في الطول.
**ثانيًا: المربع**
هو حالة خاصة من متوازي الأضلاع يجمع بين خواص المستطيل والمعين:
* كل زواياه قائمة.
* كل أضلاعه متساوية.
* أقطاره متساوية ومتعامدة.
**ثالثًا: المعين**
هو متوازي أضلاع أضلاعه الأربعة متساوية.
الخصائص:
* الأقطار متعامدة.
* كل قطر ينصف الزاوية المقابلة.
**رابعًا: متوازي الأضلاع العام**
لا يشترط فيه تساوي الزوايا أو الأضلاع سوى الضلعين المتقابلين.
**5- شروط متوازي الأضلاع**
يمكن تحديد أن الشكل هو متوازي أضلاع إذا تحقق أحد الشروط التالية:
1. كل ضلعين متقابلين متساويان.
2. كل ضلعين متقابلين متوازيان.
3. ضلعان متقابلان متساويان ومتناسبان.
4. قطراه ينصفان بعضهما.
5. زاويتان متقابلتان متساويتان.
**6- الأقطار في متوازي الأضلاع**
تعتبر **الأقطار** من أهم العناصر التي تساعد في دراسة متوازي الأضلاع.
**خصائص الأقطار:**
1. **الأقطار تنصف بعضها البعض.**
2. لا يشترط أن تكون الأقطار متساوية إلا في حالتي:
* المستطيل
* المربع
3. أقطار المعين تتعامد وتشكل أربع زوايا قائمة.
4. الأقطار تقسم الشكل إلى مثلثين متطابقين.
**7- مساحة متوازي الأضلاع**
يمكن حساب مساحة متوازي الأضلاع باستخدام أكثر من صيغة:
**أولاً: الصيغة الأساسية:**
\text{المساحة} = \text{القاعدة} \times \text{الارتفاع}
**ثانيًا: صيغة باستخدام الأضلاع والزوايا:**
\text{المساحة} = (a \times b) \times \sin(\theta)
حيث:
* *a، b* ضلعان متجاوران
* *θ* الزاوية بينهما
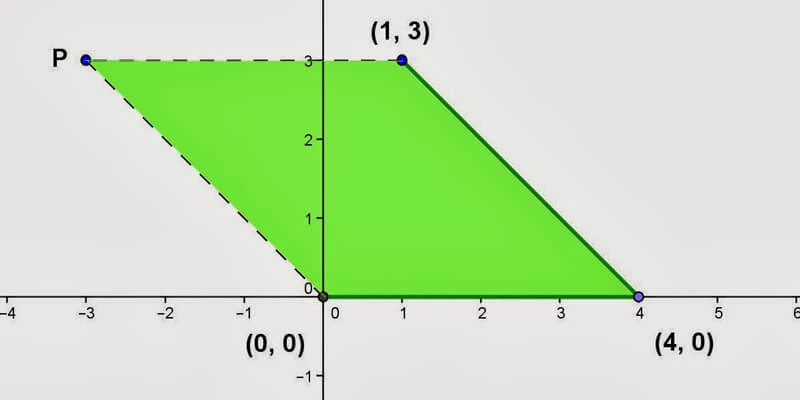
**ثالثًا: الصيغة باستخدام الإحداثيات (للأشكال المتقدمة):**
A=\left|x_1y_2 + x_2y_3 + x_3y_4 + x_4y_1 - (y_1x_2 + y_2x_3 + y_3x_4 + y_4x_1)\right| \bigg/ 2
**8- محيط متوازي الأضلاع**
يحسب المحيط بسهولة لأنه يتكون من ضلعين متساويين:
[\text{المحيط} = 2(a + b)
حيث a و b ضلعان متجاوران.
**9- الزوايا في متوازي الأضلاع**
* الزاويتان المتقابلتان **متساويتان** تمامًا.
* الزاويتان المتجاورتان **مجموعهما 180°**.
* يمكن أن يكون الشكل:
* حاد الزوايا
* قائم الزوايا
* منفرج الزوايا
**10- استخدامات متوازي الأضلاع في الحياة اليومية**
1. **تصميم السلالم والميول**
2. **تصميم النوافذ الحديدية والخشبية**
3. **الهندسة المعمارية والبناء**
4. **المسح الجغرافي ورسم الخرائط**
5. **تحليل القوى في الميكانيكا (قانون متوازي الأضلاع للقوى)**
6. **التصميم الجرافيكي وأعمال الطباعة**
7. **تحليل الأجسام القابلة للانحناء مثل الأقمشة**
**11- متوازي الأضلاع في الهندسة والرياضيات التطبيقية**
**أولاً: في الفيزياء**
قانون متوازي الأضلاع للقوى يُستخدم لدمج قوتين غير متعامدتين.
**ثانيًا: في الهندسة المدنية**
* رسم المخططات
* حساب المساحات
* تصميم الجسور والواجهات
**ثالثًا: في الرسم الهندسي**
يُستخدم لإظهار العمق في الرسومات ثلاثية الأبعاد.
**12- أمثلة محلولة**
**مثال 1:**
إذا كان طول القاعدة 12 سم، والارتفاع 5 سم، فما المساحة؟
الحل:
12 \times 5 = 60 , \text{سم}^2
**مثال 2:**
متوازي أضلاع أضلاعه 8 سم و 6 سم، والزّاوية بينهما 30°، احسب المساحة.
الحل:
(8 \times 6) \sin 30° = 48 \times 0.5 = 24 , \text{سم}^2
**مثال 3:**
طول الضلعين المتجاورين 10 سم و 7 سم. احسب المحيط.
\text{المحيط} = 2(10+7)=34 , \text{سم}
**13- الخاتمة**
يتضح مما سبق أنّ **متوازي الأضلاع** ليس مجرد شكل رباعي بسيط، بل هو عنصر هندسي أساسي له تطبيقات واسعة في العلوم المختلفة، بدءًا من الرياضيات والفيزياء إلى الهندسة والعمارة. وقد تناول البحث تعريف الشكل، وخصائصه، وأنواعه، ومساحته، ومحيطه، والأقطار والزوايا، إضافة إلى أمثلة تطبيقية.
إنّ فهم هذا الشكل يساعد بشكل مباشر على تطوير المهارات الهندسية وتسهيل دراسة الأشكال الأكثر تعقيدًا.
**14- المراجع**
1. كتاب الهندسة التحليلية – وزارة التربية والتعليم.
2. مبادئ الهندسة – الطبعة الحديثة.
3. Applied Geometry – University Textbook.
4. Geometry Essentials – High School Curriculum.
5. موقع Khan Academy – قسم Geometry.